Ever dabbled in graph theory and bumped into the challenge of determining the shortest path? Enter the Bellman-Ford Algorithm. This brilliant piece of computer science magic not only helps find the shortest path but is unique in its approach to solving problems where some of the edge weights are negative. This article breaks down how it works in the C language. Let’s dive in!
Understanding the Bellman-Ford Algorithm
The Bellman-Ford algorithm, named after Richard Bellman and Lester Ford, is a method that calculates the shortest path from a single source vertex to all other vertices in a weighted graph. What sets it apart? Unlike other algorithms, it accounts for graphs with negative weight cycles.
The Mechanics
- Initialization: All vertices are initialized with a value of infinity except for the starting vertex which is given a value of 0;
- Main Loop: The edges are relaxed |V|-1 times where |V| is the number of vertices in the graph;
- Negative Cycle Check: Post the main loop, the algorithm checks for negative weight cycles.
The Algorithm’s Strengths and Weaknesses
Before we deep dive into code snippets, knowing when to use this algorithm is key.
Strengths
- Versatility: Can handle graphs with negative weight edges;
- Preciseness: Returns a boolean value indicating the presence of a negative cycle.
Weaknesses
- Slower Than Dijkstra’s: For graphs without negative weight edges, Dijkstra’s algorithm is faster.
Bellman-Ford in C: The Code Breakdown
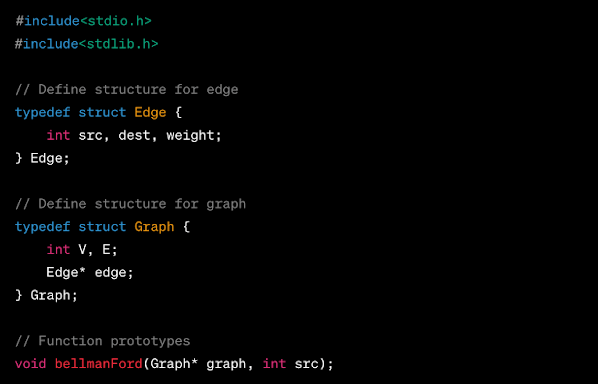
Setting Up The Graph:
We’ll start by defining a structure for the graph and the edges. A graph in our representation will be an array of edges.
The BellmanFord Function:
This function will implement the Bellman-Ford algorithm and display the shortest path.
Steps for Implementation:
- Initialization: Initialize distances from the source to all vertices as infinite and distance to the source itself as 0;
- Relaxation: Relax all edges |V| – 1 times. A simple shortest path from source to any vertex can have at-most |V| – 1 edges;
- Check for Negative Weight Cycles: After the above step, check for negative weight cycles by performing one more relaxation step on all edges. If we get a shorter path, there’s a cycle.
Handling Negative Cycles
A unique and vital aspect of the Bellman-Ford algorithm is its ability to detect negative weight cycles. If we can get a shorter path in the |V|th iteration, then there exists a negative cycle.
A Practical Use Case
Consider you’re building a currency exchange application. The Bellman-Ford algorithm can help detect arbitrage opportunities. These are instances where, due to varying currency exchange rates, you can start with an amount in one currency and, through a series of exchanges, end up with more of that same currency. The algorithm, by detecting negative cycles, can highlight these opportunities.
C++ String Comparison: Ignoring Case Sensitivity
In C++, comparing strings without considering case differences can be handy for tasks like user input validation or database searches. While there’s no built-in function for case-insensitive comparison in C++, here’s how you can do it:
Methods for Case-Insensitive String Comparison:
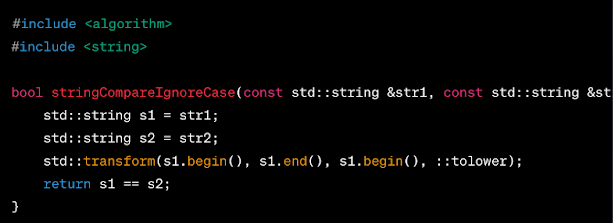
1. Using the transform() Function:
Convert both strings to lowercase using the transform() function from the STL, and then compare them.
2. Using strcasecmp():
A simpler, C-style function for direct comparison.

Quick Comparison:
| Method | Pros | Cons |
|---|---|---|
| transform() | More C++ idiomatic | Slower for large data |
| strcasecmp() | Direct & simple | Less C++ styled |
Choose the method that best aligns with your application’s needs and your coding style.
Conclusion
The Bellman-Ford algorithm in C offers a robust solution to finding the shortest paths in graphs, especially those with negative weights. Its ability to detect negative weight cycles makes it invaluable in certain scenarios. While there are faster algorithms for positive-weighted graphs, the versatility of Bellman-Ford makes it an essential tool in the programmer’s toolkit.
FAQs
Unlike most shortest path algorithms, the Bellman-Ford can handle graphs with negative weight cycles.
We relax the edges |V| – 1 times.
For graphs without negative weight edges, Dijkstra’s algorithm is generally faster.
If, after |V| – 1 relaxations, we can still find a shorter path, there’s a negative cycle.
Detecting arbitrage opportunities in currency exchange is one practical example.